今日算法之_77_灯泡开关
前言
Github:https://github.com/HealerJean
1、灯泡开关
初始时有 n 个灯泡关闭。
第 1 轮,打开所有的灯泡。
第 2 轮,每两个灯泡你关闭一次。
第 3 轮,每三个灯泡切换一次开关(如果关闭则开启,如果开启则关闭)。
第 i 轮,每 i 个灯泡切换一次开关。
对于第 n 轮,你只切换最后一个灯泡的开关。 找出 n 轮后有多少个亮着的灯泡。
示例:
输入: 3
输出: 1
解释:
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].
你应该返回 1,因为只有一个灯泡还亮着。
1.1、解题思路
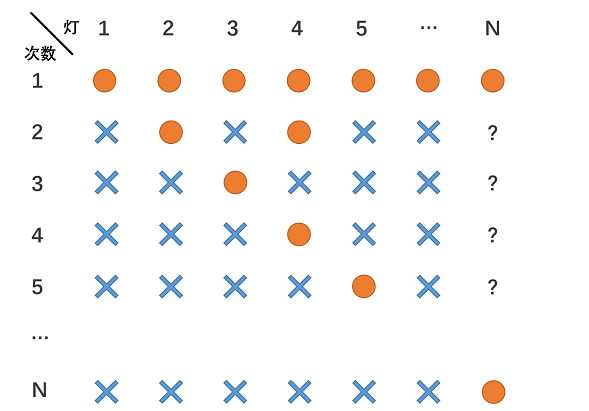
观察可知,
2的因数为 [1,2] ,第2个灯被切换了2次;
4的因数为 [1,2,4] ,第四个灯被切换了3次
题目要求,最后开着灯灯的个数,因此只有那些因数个数为奇数的灯是开着的
什么是因数:可以被整除的数就是因数,那么观察一下那些因数为奇数的灯有什么共同点,发现他们都是平方数
为什么完全平方数的因数的个数是奇数个?
设P,A,B 为正整数,如果 P=A*B,则A和B为P的因数。
P的因数A和B总是成对出现。也就是说他们总是一起为 P 的因数个数做贡献。
但是如果他们相等呢?这个时候他们一起只会为因数的个数贡献 1。
综上所述,只要找到<=n的所有完全平方数就可以了。
1.2、算法
public int bulbSwitch(int n) {
int count = 0;
for (int i = 1 ; i * i <=n ; i++){
count = i ;
}
return count;
}
1.3、测试
@Test
public void test(){
System.out.println(bulbSwitch(8));
}
2、灯泡开关
现有一个房间,墙上挂有 n 只已经打开的灯泡和 4 个按钮。在进行了 m 次未知操作后,你需要返回这 n 只灯泡可能有多少种不同的状态。
假设这 n 只灯泡被编号为 [1, 2, 3 …, n],这 4 个按钮的功能如下:
1、将所有灯泡的状态反转(即开变为关,关变为开)
2、将编号为偶数的灯泡的状态反转
3、将编号为奇数的灯泡的状态反转
4、将编号为 3k+1 的灯泡的状态反转(k = 0, 1, 2, …)
示例 1:
输入: n = 1, m = 1.
输出: 2
说明: 状态为: [开], [关]
示例 2:
输入: n = 2, m = 1.
输出: 3
说明: 状态为: [开, 关], [关, 开], [关, 关]
示例 3:
输入: n = 3, m = 1.
输出: 4
说明: 状态为: [关, 开, 关], [开, 关, 开], [关, 关, 关], [关, 开, 开].
2.1、解题思路
纯找规律

可以看看到 4和1,5和3,6和2是一致是一致的。题目是问有多少种,所以我们只分析前三种就可以了 。当大于3的时候,全部以n=3为主
| n | m | res | |
|---|---|---|---|
| 1 | 0 | 【开】 | 1 |
| 1 | 1 | 【关】, 【开】 | 2 |
| 1 | 2 | 【关】, 【开】 | 2 |
| 1 | …… | 【关】, 【开】 | 2 |
| n | m | res | |
|---|---|---|---|
| 2 | 0 | [开,开】 | 1 |
| 2 | 1 | 【关,关】,【 开,关】, 【关,开】 | 3 |
| 2 | 2 | 【开,开】, 【关,开】, 【开,关】,【 关,关】 | 4 |
| 2 | 3 | 【关,关】, 【开,关】, 【关,开,】 【开,开】 | 4 |
| 2 | …… | 【关,关】, 【开,关】, 【关,开】, 【开,开] | 4 |
| n | m | res | |
|---|---|---|---|
| 3 | 0 | 【关,关,关】 | 1 |
| 3 | 1 | 【关,关,关】,【 开,关,开】,【 关,开,关】, 关,开,开】 | 4 |
| 3 | 2 | 【开,开,开】, 【关,开,关】,【 开,关,开】【 开,关,关】, 【关,关,关】, 【关,关,开】, 【开,开,关】 | 7 |
| 3 | 3 | 【关,关,关】, 【开,关,开】, 【关,开,关】, 【关,开,开】, 【开,开,开】, 【开,开,关】, 【关,关,开】, 【开,关,关】 | 8 |
| 3 | …… | 【[开,开,开】, 【关,开,关】,【 开,关,开】, 【开,关,关】, 【关,关,关】, 【关,关,开】, 【开,开,关】, 【关,开,开】 | 8 |
2.2、算法
2.2.1、解法1
public int flipLights(int n, int m) {
n = Math.min(n, 3);
int[][] matrix = {
{1, 1, 1},
{0, 1, 0},
{1, 0, 1},
{1, 0, 0}
};
/** 获取 组合集合 */
List<ArrayList<Integer>> res = new ArrayList<>();
find(matrix, m, 0, res, new LinkedList<>());
System.out.println(res);
/** 获取所有的列表 */
List<String> collect = getStrings(n, matrix, res);
System.out.println(collect);
return collect.size();
}
/**
* 获取不重复的结果
* @param n 灯泡数量
* @param matrix
* @param res
* @return
*/
private List<String> getStrings(int n, int[][] matrix, List<ArrayList<Integer>> res) {
return res.stream().map(item -> {
// ret 为 最终位置所点击的次数
int[] value = new int[n];
for (int i = 0; i < n; i++) {
int finalI = i;
item.stream().forEach(j -> value[finalI] = matrix[j][finalI] + value[finalI]);
}
/** 偶数开,奇数关 */
return Arrays.stream(value).boxed().map(x -> x % 2 == 0 ? "开" : "关")
.collect(Collectors.collectingAndThen(Collectors.joining(","), x -> x));
}).distinct().collect(Collectors.toList());
}
/**
* 获取按m次灯泡的 组合
* @param matrix
* @param m 按多少次灯泡
* @param index
* @param res
* @param list
*/
public void find(int[][] matrix, int m, int index, List<ArrayList<Integer>> res, LinkedList<Integer> list){
/** 找到5次的 */
if(list.size() == m){
res.add(new ArrayList(list));
return;
}
/** 用过就不会回头,但是可以多次使用,所以是index */
for (int i = index ; i < matrix.length ; i++){
list.add(i);
find(matrix,m,i, res,list);
list.removeLast();
}
}
2.2.2、解法2,找规律
public int flipLight1(int n, int m) {
n = Math.min(n, 3);
//不按开关
if (m == 0){
return 1 ;
}
//m > 0 的时候
if (n == 1){
return 2 ;
}
if (n == 2){
return m == 1 ? 3 : 4 ;
}
return m == 1 ? 4 : m==2 ? 7 : 8 ;
}
2.3、测试
@Test
public void test(){
System.out.println(flipLights(1,1));
}


