By

前言

Github：https://github.com/HealerJean

博客：http://blog.healerjean.com

1、从中序与后序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意：你可以假设树中没有重复的元素。

前序遍历 preorder = [3,9,20,15,7]

中序遍历 inorder = [9,3,15,20,7]


    3
   / \
  9  20
    /  \
   15   7

1.1、解题思路

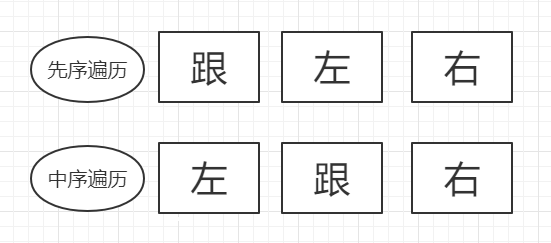
image-20200525112215394

1.2、算法

  public TreeNode buildTree(int[] preorder, int[] inorder) {
        Map<Integer, Integer> hashMap = new HashMap(inorder.length);
        for (int i = 0; i < inorder.length; i++) {
            hashMap.put(inorder[i], i);
        }

        return createTree(preorder, inorder, 0, preorder.length-1, 0, inorder.length-1,  hashMap);
    }

    public TreeNode createTree(int[] preorder, int[] inorder, 
                               int p_left_index, int p_right_index, 
                               int in_left_index, int in_right_index , 
                               Map<Integer, Integer> hashMap) {
        
        if (p_left_index > p_right_index || in_left_index > in_right_index) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        // 先把中序遍历 中的  根节点找到，然后以这个节点开始创建左右节点
        TreeNode root = new TreeNode(preorder[p_left_index]);

        // 在中序遍历中定位根节点
        // 当然也可以使用map，这样就不用每次都使用for循环读取了
        // int in_root_index = 0 ;
        // for(int i = 0 ; i < inorder.length ; i++){
        //     if (inorder[i] == root.val){
        //         in_root_index = i ;
        //     }
        // }
        int in_root_index = hashMap.get(preorder[p_left_index]);

        // 得到左子树中的节点数目
        int size = in_root_index - in_left_index;

        root.left = createTree(preorder, inorder, 
                               p_left_index + 1, p_left_index + size, 
                               in_left_index, in_root_index - 1, 
                               hashMap);
        
        root.right = createTree(preorder, inorder, 
                                p_left_index + size + 1, p_right_index, 
                                in_root_index + 1, in_right_index, 
                                hashMap);
        return root;
    }




    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int x) {
            val = x;
        }
        TreeNode(int x, TreeNode left, TreeNode right) {
            this.val = x;
            this.left = left;
            this.right = right;

        }
    }

1.3、测试


    @Test
    public void test(){
        int[] preorder = {3,9,20,15,7} ;
        int[] inorder = {9,3,15,20,7} ;

        System.out.println(buildTree(preorder, inorder));
    }

2、从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意：你可以假设树中没有重复的元素。

中序遍历 inorder = [9,3,15,20,7]

后序遍历 postorder = [9,15,7,20,3]


    3
   / \
  9  20
    /  \
   15   7

2.1、解题思路

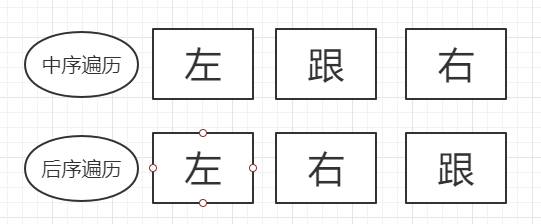
image-20200525112555970

2.2、算法


public TreeNode buildTree(int[] inorder, int[] postorder) {

    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0 ; i <  inorder.length; i++){
        map.put(inorder[i], i);
    }
    return createTree(map ,inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1);

}

public TreeNode createTree(Map<Integer, Integer> map ,
                           int[] inorder, int[] postorder, 
                           int in_left_index, int in_right_index, 
                           int post_left_index, int post_right_index) {
    
    if (in_left_index >= in_right_index || post_left_index >= post_right_index){
        return null ;
    }

    TreeNode root = new TreeNode(post_right_index);

    Integer  in_root_index = map.get(postorder[post_right_index]);
    int size = in_root_index - in_left_index ;

    root.left =  createTree(map ,inorder, postorder, 
                            in_left_index , in_root_index - 1, 
                            post_left_index, post_left_index + size  -1) ;

    root.right =  createTree(map ,inorder, postorder, 
                             in_root_index+1, in_right_index, 
                             post_left_index + size , post_right_index) ;
    return root ;
}

2.3、测试

@Test
public void test(){
    int[] inorder = {9,3,15,20,7} ;
    int[] postorder = {9,15,7,20,3} ;

    System.out.println(buildTree(inorder, postorder));
}

​

ContactAuthor