今日算法之_20_寻找两个有序数组的中位数
前言
Github:https://github.com/HealerJean
1、寻找两个有序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
1.1、解题思路
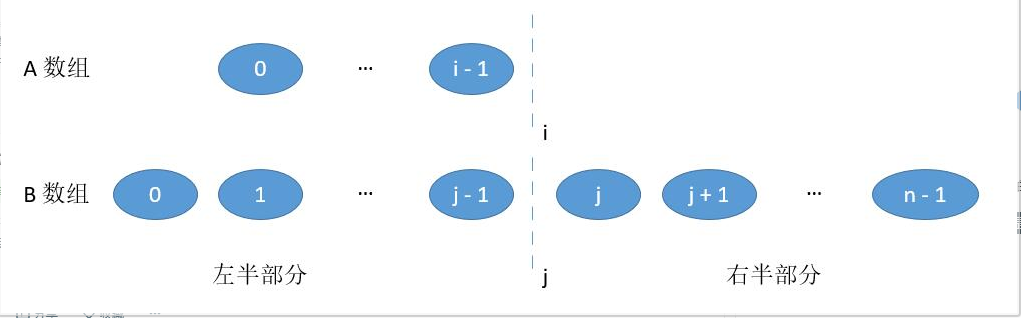
我们把
数组 A和数组 B分别在i和j进行切割。 如下图所示
将 i 的左边和 j 的左边组合成「左半部分」,将 i 的右边和 j 的右边组合成「右半部分」。
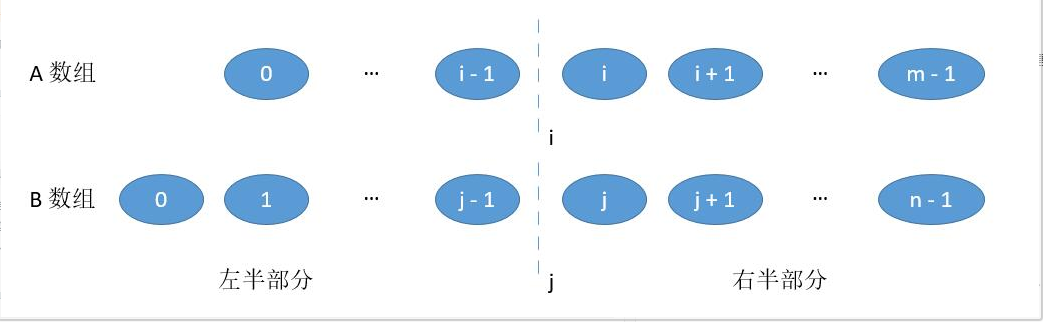
情况一:当 A 数组和 B 数组的总长度是偶数时 ,必须保证如下
1、左半部分的长度等于右半部分
i + j = m - i + n - j 推导出=》 j = ( m + n ) / 2 - i
2、左半部分最大的值小于等于右半部分最小的值: max (A [i-1],B [j-1]) <= min (A [i], B [j])
中位数 = (左半部分最大值 + 右半部分最小值 )/ 2。
中位数 = (max (A [i - 1] , B [j - 1]+ min (A [i], B [j])) / 2
情况二:当 A 数组和 B 数组的总长度是奇数时,必须保证如下
1、左半部分的长度比右半部分大 1
i + j = m - i + n - j + 1 推导出=》 j = ( m + n + 1) / 2 - i
2、左半部分最大的值小于等于右半部分最小的值: max (A [i-1],B [j-1]) <= min (A [i], B [j]),同情况一第二个条件
中位数 = 左半部分最大值(左半部比右半部分多出的那一个数)
中位数 = max ( A [ i - 1 ] , B [ j - 1 ])
情况分析/条件汇总:
1、第一个条件,因为m+n是偶数,其实可以写成成 j = ( m + n + 1) / 2 - i,这样就可以情况二的第一个条件相同了。 又由于 0 <= i <= m,因为j和i的关系是有公式推导的,为了保证 0 <= j <= n,有如下方程

2、对于第二个条件 : max ( A [ i - 1 ] , B [ j - 1 ])) <= min ( A [ i ] , B [ j ])),我们只要保证以下4个条件
A [ i - 1 ] <= A [ i ]
A [ i - 1 ] <= B [ j ]
B [ j - 1 ] <= B [ j ]
B [ j - 1 ] < = A [ i ]
但是我们可以看到其实A [ i - 1 ] <= A [ i ] 和B [ j - 1 ] <= B [ j ] 因为数组是有序的,所以是必然的,所以我们只要保证其他两种就可以了,如下
A [ i - 1 ] <= B [ j ]
B [ j - 1 ] <= B [ j ]
分两种情况讨论
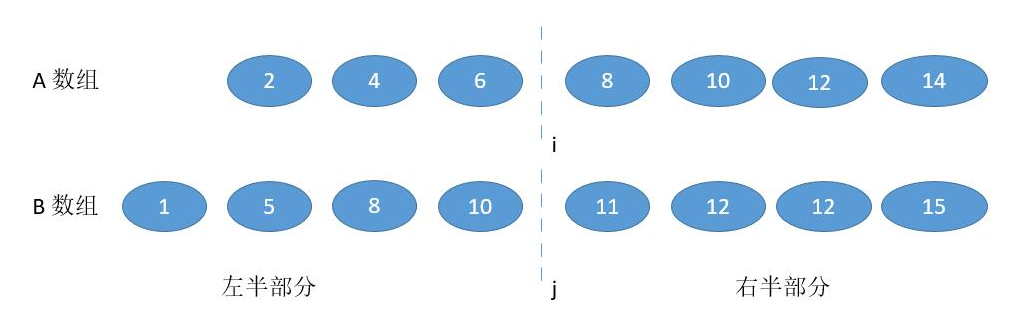
1、B [ j - 1 ] > A [ i ],并且为了不越界,要保证 j != 0,i != m
通过仔细观察(10 > 8 ),我们需要增加 i ,为了数量的平衡还要减少 j ,幸运的是 j = ( m + n + 1) / 2 - i,i 增大,j 自然会减少。
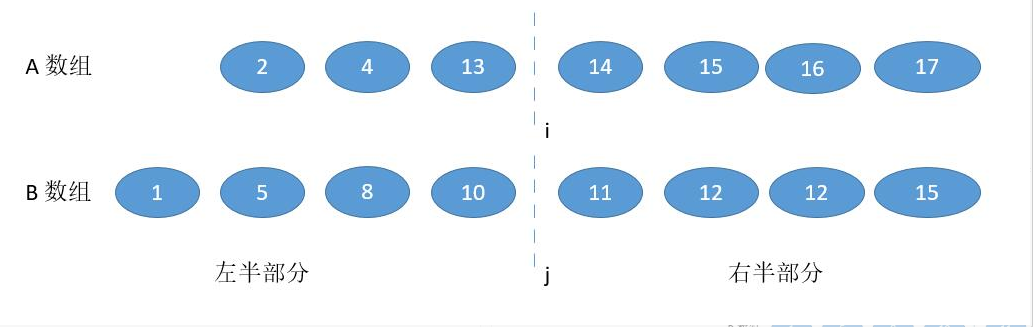
2、A [ i - 1 ] > B [ j ] ,并且为了不越界,要保证 i != 0,j != n
此时和上边的情况相反,(13 > 11 ),我们要减少 i ,增大 j 。
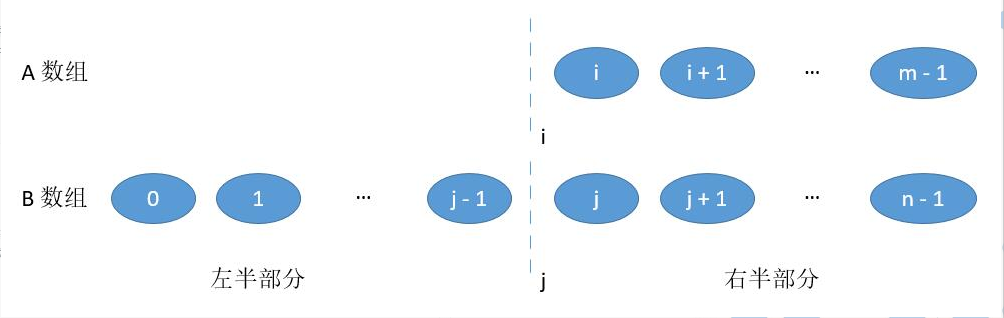
3、上面的两种情况,我们把边界都排除了
3.1、当 i = 0, 或者 j = 0,也就是切在了最前边。
左半部分:
当 j = 0 时,最大的值就是 A [ i - 1 ] ;
当 i = 0 时 最大的值就是 B [ j - 1] ;
右半部分最小值和之前一样 :
min (A [i], B [j])
3.2、当 i = m 或者 j = n,也就是切在了最后边。
左半部分最大值和之前一样:
max(A [i - 1], B [j - 1])右半部分:
j = n 时, 最小值就是 A [ i ] ;
i = m 时,最小值就是B [ j ] 。
所有的思路都理清了,最后一个问题,增加 i 的方式。当然用二分了(看到上面的log(m+n),也可以认为要用二分了),初始化 i 为中间的值,然后减半找中间的,减半找中间的,减半找中间的直到答案。
1.2、算法
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
//如果数组 A 比较长,则交换 A、B 数组
if (m > n) {
return findMedianSortedArrays(B, A);
}
//增加i的方式使用折半查找
int iMin = 0, iMax = m;
while (iMin <= iMax) {
//i 折半查找中间值
int i = (iMin + iMax) / 2;
int j = (m + n + 1) / 2 - i;
// i 需要增大
//数组 A 分割点相邻左边那个元素比数组 B 分割点相邻右边那个元素大,则应该将数组 A 分割点向右移,数组 B 分割点向左移
//数组 A 分割点有向左移趋势,需检查左边界
if (j != 0 && i != m && B[j - 1] > A[i]) {
iMin = i + 1;
// i 需要减小
//数组 A 分割点相邻右边那个元素比数组 B 分割点相邻左边那个元素大,则应该将数组 A 分割点向左移,数组 B 分割点向右移
//数组 A 分割点有向右移趋势,需检查右边界
} else if (i != 0 && j != n && A[i - 1] > B[j]) {
iMax = i - 1;
// 达到要求,并且将边界条件列出来单独考虑
} else {
int maxLeft = 0;
if (i == 0) {
maxLeft = B[j - 1];
} else if (j == 0) {
maxLeft = A[i - 1];
} else {
maxLeft = Math.max(A[i - 1], B[j - 1]);
}
// 奇数的话不需要考虑右半部分(因为奇数的话,左面自然就多了一个数字)
if ((m + n) % 2 == 1) {
return maxLeft;
}
int minRight = 0;
if (i == m) {
minRight = B[j];
} else if (j == n) {
minRight = A[i];
} else {
minRight = Math.min(B[j], A[i]);
}
//如果是偶数的话返回结果
return (maxLeft + minRight) / 2.0;
}
}
return 0;
}
1.3、测试
@Test
public void test() {
int[] A = new int[]{1, 3};
int[] B = new int[]{2};
System.out.println(findMedianSortedArrays(A, B));
}
2


