今日算法之_18_动态规划之_1_爬楼梯_2_国王和金矿_3_交叉队列
前言
Github:https://github.com/HealerJean
1、动态规划 (感谢程序员小灰)
动态规划宗旨:大事化小,小事化了
1、爬楼梯
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。
1.1、递归算法
这个问题其实我们仔细思考,到最后的第10层楼梯,事实上只有2种走法,就是从9级上10层(一步一层)、8级上10层(一步2层)。 所以应该是F(10) = F(9) + F(8) 的结果。这是不是马上就可以得出结果呢 。通过下面的代码执行后有89种方法
@Test
public void method(){
System.out.println(f(10));//89
}
public int f(int n){
//第1级台阶有1中走法
if (n == 1){
return 1 ;
}
//第2级台阶有两种走法
if (n == 2){
return 2;
}
//其他台阶的走法是 如下
return f(n-1) + f(n-2);
}
1.2、优化递归算法-添加备忘录
优化该算法:上面的时间复杂度我们先求一下 ,要算出F(n),我们先必须知道F(n-1)和F(n-2),要算F(n-1),就必须算F(n-2) 和 F(n-3)的值,依次类推 ,我们可以得到下面的图
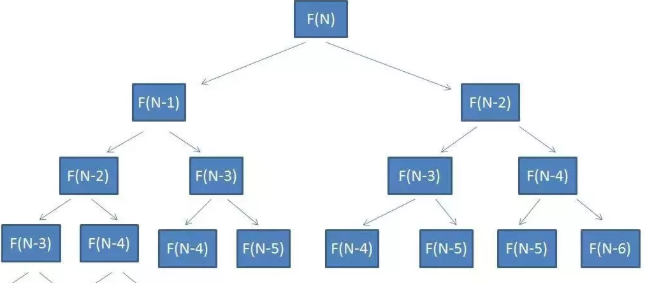
所以时间复杂度 应该是2^n - 1 约等于2^n , 这个时候我们看到上面重复计算的还是挺多的,比如下面相同颜色的都被重新计算了。 我们可以保存一下已经计算过的东西,如果计算过,就不让它重新计算了,
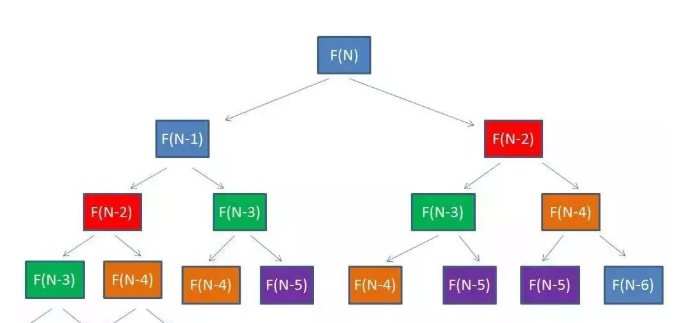
这个时候,我加一个备忘录算法,保存一下当时的计算状态 ,集合map是一个备忘录。当每次需要计算F(N)的时候,会首先从map中寻找匹配元素。如果map中存在,就直接返回结果,如果map中不存在,就计算出结果,存入备忘录中。,调整代码后如下
@Test
public void method2() {
Map<Integer, Integer> map = new HashMap<>();
System.out.println(f2(10, map));
}
public int f2(Integer n, Map<Integer, Integer> map) {
//第1级台阶有1中走法
if (n == 1) {
return 1;
}
//第2级台阶有两种走法
if (n == 2) {
return 2;
}
Integer value = map.get(n);
if (value == null) {
//其他台阶的走法是 如下
value = f2(n - 1, map) + f2(n - 2, map);
map.put(n, value);
return value;
}
return value;
}
这个算法时间时间复杂度的话,F1到F(n),除了n=1,n=2,基本上每次都会进入map中,也就是说最后的map中一共存放了n-2个结果,那么时间复杂度就是n
1.3、动态规划求解
1.3.1、动态规划3个重要概念
最优子结构、边界、状态转移公式
F(10) = F(9) + F(8):最优子结构
当只有1级台阶或者2级台阶的时候,我们可以得到结果了,而且无需简化了再。我们称之为边界
F(n) = F(n-1)+F(n-2):这个是阶段与阶段之间的状态转移方程,这个是动态规划的核心
从下到上推广
**其实递归算法到了这里基本上时间复杂度不能再优化了,但是空间复杂度我们还可以优化,现在是map存储的数据,数据量其实是比较多的, **
递归算法是从上到下进行递归的,那我们可不可以从下到上进行推导呢 ,就是说从1级台阶开始从下到上推 F(1) = 1,F(2) = 2,F(3) = F(1) +F(2),F(4) = F(3) +F(2), 等等等
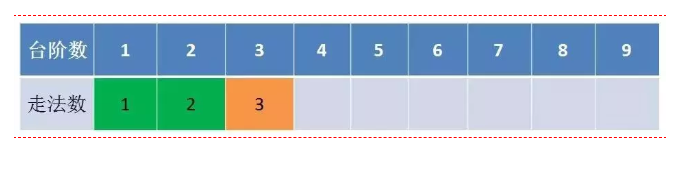
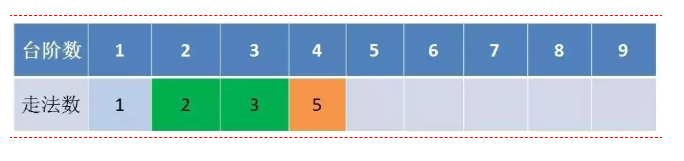
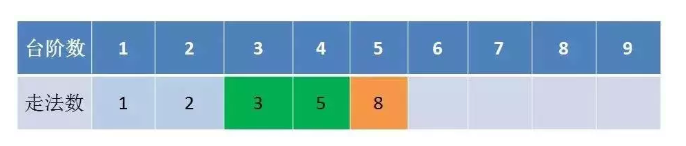
这样下来,其实只要我们保留之前两个状态就可以一直推导到第10个了,这才是真正的动态实现哦,
代码解析:程序从 i=3 开始迭代,一直到 i=n 结束。每一次迭代,都会计算出多一级台阶的走法数量。迭代过程中只需保留两个临时变量a和b,分别代表了上一次和上上次迭代的结果。 为了便于理解,我引入了temp变量。temp代表了当前迭代的结果值。
@Test
public void method3() {
System.out.println(f3(10));
}
public int f3(int n) {
//第1级台阶有1中走法
if (n == 1) {
return 1;
}
//第2级台阶有两种走法
if (n == 2) {
return 2;
}
//从3级台阶开始,每次都等于前两级,相加,a是倒数第2级,b是倒数第1级
int a = 1;
int b = 2;
int temp = 0;
for (int i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}
这个算法的时间复杂度是O(n),但是空间复杂度值引入了3个变量,空间复杂度竟然只有1,简直牛掰了,但是这才只是比较简单的动态规划,还不算真正理解动态规划
2、国王和金矿
问题:有一个国家发现了5座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半金矿。要求用程序求解出,要想得到尽可能多的黄金,应该选择挖取哪几座金矿?
1)挖每一座金矿需要的人数是固定的,多一个人少一个人都不行。国王知道每个金矿各需要多少人手.
2)每一座金矿所挖出来的金子数是固定的.
3)开采一座金矿的人完成开采工作后,他们不会再次去开采其它金矿,因此一个人最多只能使用一次.
| 金矿编号 | 黄金储量 | 需要人数 |
|---|---|---|
| 1 | 400 | 5 |
| 2 | 500 | 5 |
| 3 | 200 | 3 |
| 4 | 300 | 4 |
| 5 | 350 | 3 |
2.1、确定最优子结构
不考虑人数够不够用,也不考虑到底挖不挖,第5个金矿存在挖与不挖的问题 。当然我们希望是全挖的,但是工人数有限制,所以可能存在不挖的情况 。这样就会出现2中最优子结构 ,最优子结构有两种,
一种是5金矿10工人,
一种是4金矿10工人。
如果选挖第五个金矿,那么前4个金矿所分配的工人就是【10 - 第五个金矿所需人数】
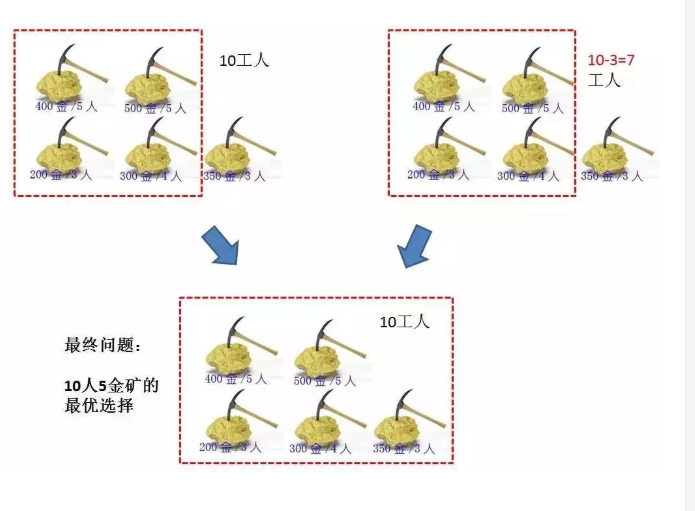
所以最优选择是:(前4个金矿10工人的挖金数量 )和 (前4个金矿7个工人+第4个金矿的挖金数量 )中的最大值
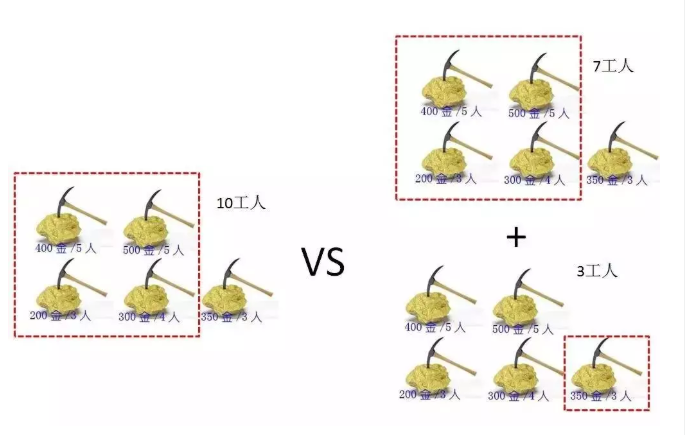
2.2、确定边界
为了便于描述,我们将金矿数量设置为N,工人数设为W,金矿的黄金量设为G[],金矿的工人用量设为数组P[]
那么5座金矿的最优选择是F(5,10) = MAX(F(4,10), F(4,10 - P[4]) + G[4])
F(n,w) 的解释为n个金矿,w个人的黄金量 (n个金矿不一定全部都挖,w个人也不一定全用)
现在我们确定下最终的边界吧,也就是最后剩下1个金矿的情况,这时存在挖与不挖的可能,因为人数可能已经分完了,如果人数分完了,那第一个金矿就不能挖了。
当n = 1 ; w < P[0]; F(n, w) = 0 ;
当n = 1 ; w >= P[0]; F(n. w) = G[0] ;
//通过上面推导出来的 n-1为当前的金矿
当n > 1 ; w < P[n - 1]; F(n, w) = F(n - 1, w) ;
当n > 1 ; w >= P[n - 1]; F(n, w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) ;
2.3、方案实现
2.3.1、递归实现
@Test
public void diGuimethod() {
int g[] = new int[]{400, 500, 200, 300, 350};//黄金量
int p[] = new int[]{5, 5, 3, 4, 3};//人数
int maxGold = diguiMaxGold(5, 10, g, p);
System.out.println(maxGold);
}
/**
* 递归算法
*/
public int diguiMaxGold(int n, int w, int[] g, int[] p) {
//n 等于 1 的情况
if (n == 1 && w < p[0]) {
return 0;
} else if (n == 1) {
return g[0];
}
//n 大于 1 的情况
if (w < p[n - 1]) {
return diguiMaxGold(n - 1, w, g, p);
}
//挖4座金矿
int a = diguiMaxGold(n - 1, w, g, p);
//挖5座金矿
int b = diguiMaxGold(n - 1, w - p[n - 1], g, p) + g[n-1];
return Math.max(a, b);
}
2.3.2、动态规划
2.3.2.1、规划过程
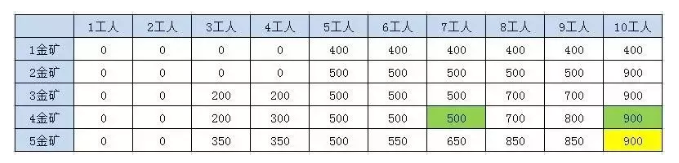
表格第一列表示给定1-5座金矿的情况,也就是n的值,表格第一行给定的工人数也就是w的值
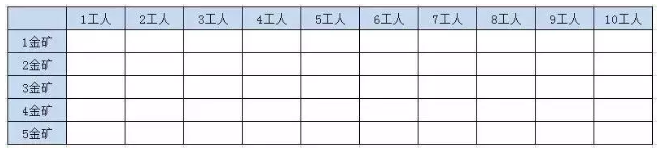
2.3.2.1.1、第1座金矿结果
第一座金矿需要的人数是5人,所以当人数小于5的时候,不会挖矿,挖金量为0
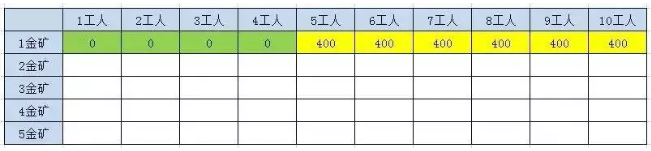
2.3.2.1.2、第2座金矿结果
当n > 1 ; w < P[n - 1]; F(n, w) = F(n - 1, w) ;
当n > 1 ; w >= P[n - 1]; F(n, w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) ;**第二座金矿需要的工人数也是5人 **
1、当人数小于5的时候,不会挖矿,挖金量为0
2、当人数在5到9人的区间,人数不足以挖取两个金矿,只能挖一个矿
3、当人数等于 碰巧1号金矿也能挖取,所以我们必须同时考虑
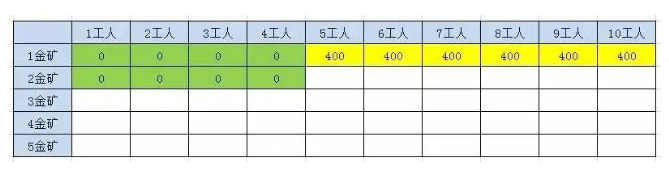
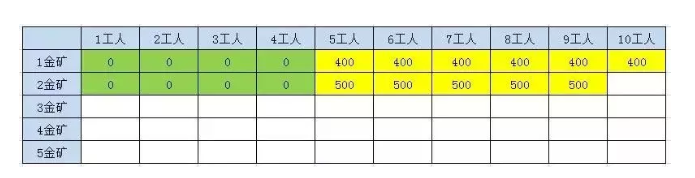
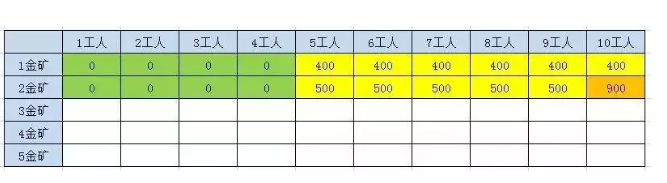
2.3.2.1.3、第3座金矿结果
n > 1F(n , w) = max(F(n-1, w), F(n-1,w-p[n-1] + g[n-1]));
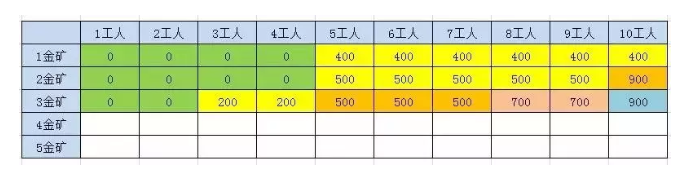
2.3.2.1.4、第4座金矿结果
n > 1F(n , w) = max(F(n-1, w), F(n-1,w-p[n-1] + g[n-1]));
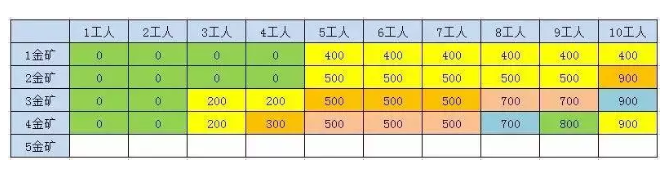
2.3.2.1.5、第5座金矿结果
n > 1F(n , w) = max(F(n-1, w), F(n-1,w-p[n-1] + g[n-1]));
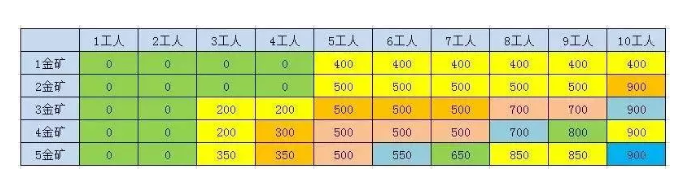
2.3.2.2.、规律总结
这个时候,我们发现,除了第一个格子之外,每个格子都是前一行的一个格子或者两个格子推出来的
比如3金矿8工人的结果,第三个金矿需要3个工人,挖的金矿数是200, 就来自2金矿5工人和2金矿8工人 Max(500,500+200) = 700
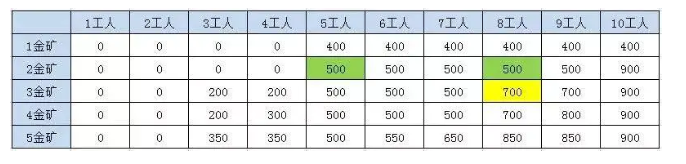
比如5金矿和10工人 来自4金矿7工人和4金矿10工人Max(900,500+350) = 900
2.3.2.3、动态规范代码
在实现程序的时候,我们也可以像这样从左至右,从上到下一格一格推导出最终结果。
但是我们并不需要存储整个表格,只需要存储前面一行的结果,就可以推导出新的一行。我们来实现一下代码。
@Test
public void method() {
int g[] = new int[]{400, 500, 200, 300, 350};//黄金量
int p[] = new int[]{5, 5, 3, 4, 3};//人数
int maxGold = getMostGold(5, 10, g, p);
System.out.println(maxGold);
}
/**
* @param n 第几个金矿
* @param w 总共有几个人
* @param g 数组,存放每个金矿的黄金数
* @param p 数组,存放每个金矿需要的工人数
* @return
*/
public static int getMostGold(int n, int w, int[] g, int[] p) {
//存放上一行的结果
int[] preResults = new int[w +1];
//存放当前行的结果
int[] results = new int[w + 1];
//填充边界格子的值
//保存的是第一行的数据
for (int i = 1; i <= w; i++) {
if (i < p[0]) {
preResults[i] = 0;
} else {
preResults[i] = g[0];
}
}
//填充其余格子的值,从上一行推出下一行,外层循环是金矿数量,内层循环是工人数
//内层循环工人数从第二行数据开始,所以i = 1
for (int i = 1; i < n; i++) {
for (int j = 1; j <= w; j++) {
//p[i] 当前金矿的人数 g[i] 当前金矿的数量
// 如果当前人数小于金矿,则最多挖的金矿数量等于相同人数 的上一层金矿的数量
if (j < p[i]){
results[j] = preResults[j];
}else {
int a = preResults[j];
int b = preResults[j - p[i]] + g[i];
results[j] = Math.max(a, b) ;
}
}
for (int j = 1; j <= w; j++) {
preResults[j] = results[j];
}
}
return results[w];
}
3、交叉队列
问题:给出三个队列 s1,s2,s3 ,判断 s3 是否是由 s1 和 s2 交叉得来。 如:s1 为 aabcc , s2 为 dbbca。 当 s3 为 aadbbcbcac 时,返回 true(即将 s1 拆成三部分: aa,bc,c 分别插入 s2 对应位置) 否则返回 false。
3.1、解题思路
1、动态规划求解,构造一个长为 len2=s2.size()+1,宽为 len1=s1.size()+1 的 dp[][] 二维数组;
2、设有 i,j,其中 i 表示字符串 s1的第 i 个字符, j 表示字符串 s2的第 j 个字符, t=i+j表示 s3的第 t 个字符;
3、dp[i][j] 如果为 1 ,表示 s1[i] 等于 s3[t] 且 dp[i−1][j] 等于 1、 或者 s2[j] 等于 ` s3[t] 且 dp[i][j−1] `;
4、简单的说 dp[i][j] 为 1 , 就表示这个点可达,以 dp[0][0] 为起点, dp[len1][len2] 为终点,dp数组中值为 1 , 的点为路径,向下走表示取 s1 的字符,向右走表示取 s2 的字符。这样就将抽象的字符组合转化成了更好理解的二维数组来表示;
5、最优子结构即为: s1,s2 的 i,j 点字符之前的字符能否交叉组合成字符串 s3 的前 i+j个字符,转换到二维数组即为, i,j 点左侧点和上方的点是否可达。
6、可以根据例1画出二维表格,便于分析:
| s2/s1 | * | d | b | b | c | a |
|---|---|---|---|---|---|---|
| * | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 1 | 1 | 1 | 1 | 1 | 0 |
| b | 0 | 1 | 1 | 0 | 1 | 0 |
| c | 0 | 0 | 1 | 1 | 1 | 1 |
| c | 0 | 0 | 0 | 1 | 0 | 1 |
3.2、代码实现
初始化的数组,数据都为0
1、先将第一行和第一列的数据初始化
2、然后从 i=1,j=1,开始扩散,首先想明白的是,如果dp[i][j] ,j相同 dp[i -1][j]= 0 ,那么 dp[i][j]= 0,所以千万注意下面 | 或的用法
@Test
public void test(){
System.out.println(method());
}
public String method() {
String line = "aabcc,dbbca,aadbbcbcac";
String[] arr1 = line.split(",");
int len1 = arr1[0].length();
int len2 = arr1[1].length();
int len3 = arr1[2].length();
//判断基本的关系
if (len3 != len1 + len2) {
return false + "";
}
if (len1 == 0) {
return (arr1[1] == arr1[2]) + "";
}
if (len2 == 0) {
return (arr1[0] == arr1[2]) + "";
}
//开始真正代码
int[][] dp = new int[len1 + 1][len2 + 1];
//第一个点必然可达
dp[0][0] = 1;
// 初始化数组第1列, 如果第第一列有一个为0,那么肯定不可达, 后续的都为0,此处代码甚好
for (int i = 1; i <= len1; i++) {
if (arr1[0].charAt(i - 1) == arr1[2].charAt(i - 1)) {
dp[i][0] = dp[i - 1][0];
}
}
//初始化数组第1hang
for (int i = 1; i <= len2; i++) {
if (arr1[1].charAt(i - 1) == arr1[2].charAt(i - 1)) {
dp[0][i] = dp[0][i - 1];
}
}
// dp
for (int i = 1; i < len1 + 1; i++) {
for (int j = 1; j < len2 + 1; j++) {
int t = i + j;
//下面这两个判断,相当于我们已经默认了,第一个数据是arr1[1] 的第一个子母,而这个子母在上面已经初始化了
if (arr1[0].charAt(i - 1) == arr1[2].charAt(t - 1)) {
dp[i][j] = dp[i - 1][j] | dp[i][j];
}
if (arr1[1].charAt(j - 1) == arr1[2].charAt(t - 1)) {
dp[i][j] = dp[i][j - 1] | dp[i][j];
}
}
}
// 返回处理后的结果
if (dp[len1][len2] == 1) {
return true + "";
}
return false + "";
}


