/**
* 打印节点数值
*/
public static void printNode(Node node) {
    System.out.print(node.getData()+ " ");
}

/**
* 初始化二叉树：
* 必须逆序简历，先建立子节点，再逆序往上建立，因为非叶子节点会使用到下面的节点，而初始化是按顺序初始化得，不逆序建立会报错
*/
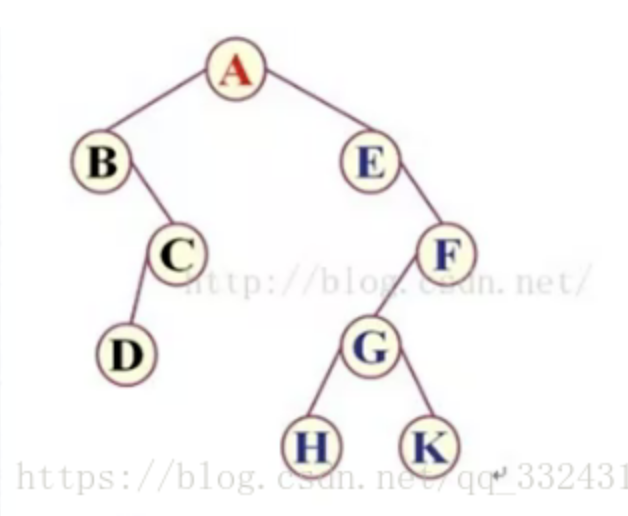
public static Node init() {
    Node H = new Node("H", null, null);
    Node K = new Node("K", null, null);
    Node G = new Node("G", H, K);
    Node F = new Node("F", G, null);
    Node E = new Node("E", null, F);
    Node D = new Node("D", null, null);
    Node C = new Node("C", D, null);
    Node B = new Node("B", null, C);
    Node A = new Node("A", B, E);
    return A;
}

@Data
public static class Node {
    private String data;
    private Node leftNode;
    private Node rightNode;

    public Node(String data, Node leftNode, Node rightNode) {
        this.data = data;
        this.leftNode = leftNode;
        this.rightNode = rightNode;
    }

}

/**
* 先序遍历（根左右）：递归
*/
public  void preOrder(Node root) {

    //1、打印根节点
    printNode(root);

    //2、使用递归遍历左孩子
    if (root.getLeftNode() != null) {
        preOrder(root.getLeftNode());
    }

    //3、使用递归遍历右孩子
    if (root.getRightNode() != null) {
        preOrder(root.getRightNode());
    }
}

@Test
public void test() {
    System.out.println("先序遍历");
    Node node = init();
    preOrder(node);
}

/**
*  先序遍历（根左右）：非递归
*  思想：栈的解决方式（后进先出，先进后出）
*/
public static void preStack(Node node) {
    // 1、初始化一个栈
    Stack<Node> stack = new Stack<>();
    // 2、判断节点不为NULL，或者栈不为空
    while (node != null || !stack.isEmpty()) {

        // if (node != null) { 目的是为了打压跟节点和左子树
        if (node != null) {
            //先打印跟节点
            printNode(node);
            //根节点放入 栈中,放到栈中的目的
            stack.push(node);
            //设置循环节点为当前节点的左子树
            node = node.getLeftNode();

            //目的是为了从栈里面取出节点
        } else {
            node = stack.pop();
            //设置循环节点为当前节点的右子树
            node = node.getRightNode();
        }
    }
}

@Test
public void test() {
    System.out.println("先序遍历");
    Node node = init();
    System.out.println();
    preStack(node);
}

/**
*
* 中序遍历（左根右） ：递归
*/
public void inOrder(Node root) {
    //使用递归遍历左孩子
    if (root.getLeftNode() != null) {
        inOrder(root.getLeftNode());
    }

    //打印根节点
    printNode(root);

    //使用递归遍历右孩子
    if (root.getRightNode() != null) {
        inOrder(root.getRightNode());
    }
}

@Test
public void test() {
    System.out.println("中序遍历");
    Node node = init();
    inOrder(node);
}

   /**
     * 中序遍历（左根右） ：非递归
     * 栈的解决方式：后进先出，先进后出
     */
    public void inStack(Node node) {
        Stack<Node> stack = new Stack<Node>();
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                //后进先出，讲所有的左子树和跟节点依次放入
                stack.push(node);
                node = node.getLeftNode();
            }
            //消化队列中的数据
            if (!stack.isEmpty()) {
                node = stack.pop();
                printNode(node);
                node = node.getRightNode();
            }
        }
    }

@Test
public void test() {
    System.out.println("中序遍历");
    Node node = init();
    inStack(node);
}

/**
*
* 后续遍历(左右根) ：递归
*/
public static void postOrder(Node root) {

    if (root.getLeftNode() != null) {
        postOrder(root.getLeftNode());
    }
    if (root.getRightNode() != null) {
        postOrder(root.getRightNode());
    }
    printNode(root);
}

  @Test
    public void test() {
        System.out.println("中序遍历");
        Node node = init();
        postOrder(node);
    }

   /**
     * 层序遍历（上到下，从从右到左）：
     * 队列的解决方案，先进先出
     */
    public static void rightToLeft(Node root) {
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            //表示每行有多少个
            int hangSize = queue.size();
            //遍历每行的数据
            while (hangSize > 0) {
                //从队列中取出，打印根节点
                Node node  = queue.remove();
                printNode(node);
                hangSize--;

                if (node.getRightNode() != null) {
                    queue.add(node.getRightNode());
                }
                if (node.getLeftNode() != null) {
                    queue.add(node.getLeftNode());
                }
            }
        }
    }




    /**
     * 层序遍历（上到下，从从左到右）：
     * 队列的解决方案，将每一行的数据放到队列中，依次打印出来
     */
    public void leftToRigit(Node root) {
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int i = queue.size();
            while (i > 0) {
                Node node = queue.remove();
                printNode(node);
                i--;
                if (node.getLeftNode() != null) {
                    queue.add(node.getLeftNode());
                }
                if (node.getRightNode() != null) {
                    queue.add(node.getRightNode());
                }
            }
        }
    }

@Test
public void test() {
    Node root = init();
    System.out.println("层序遍历 从上到下，从右到左");
    rightToLeft(root);
    System.out.println();
    System.out.println("层序遍历 从上到下，从左到右");
    leftToRigit(root);
}

    
层序遍历 从上到下，从右到左
A E B F C G D K H 
层序遍历 从上到下，从左到右
A B E C F D G H K