深入理解排序算法
前言
Github:https://github.com/HealerJean
1、排序算法
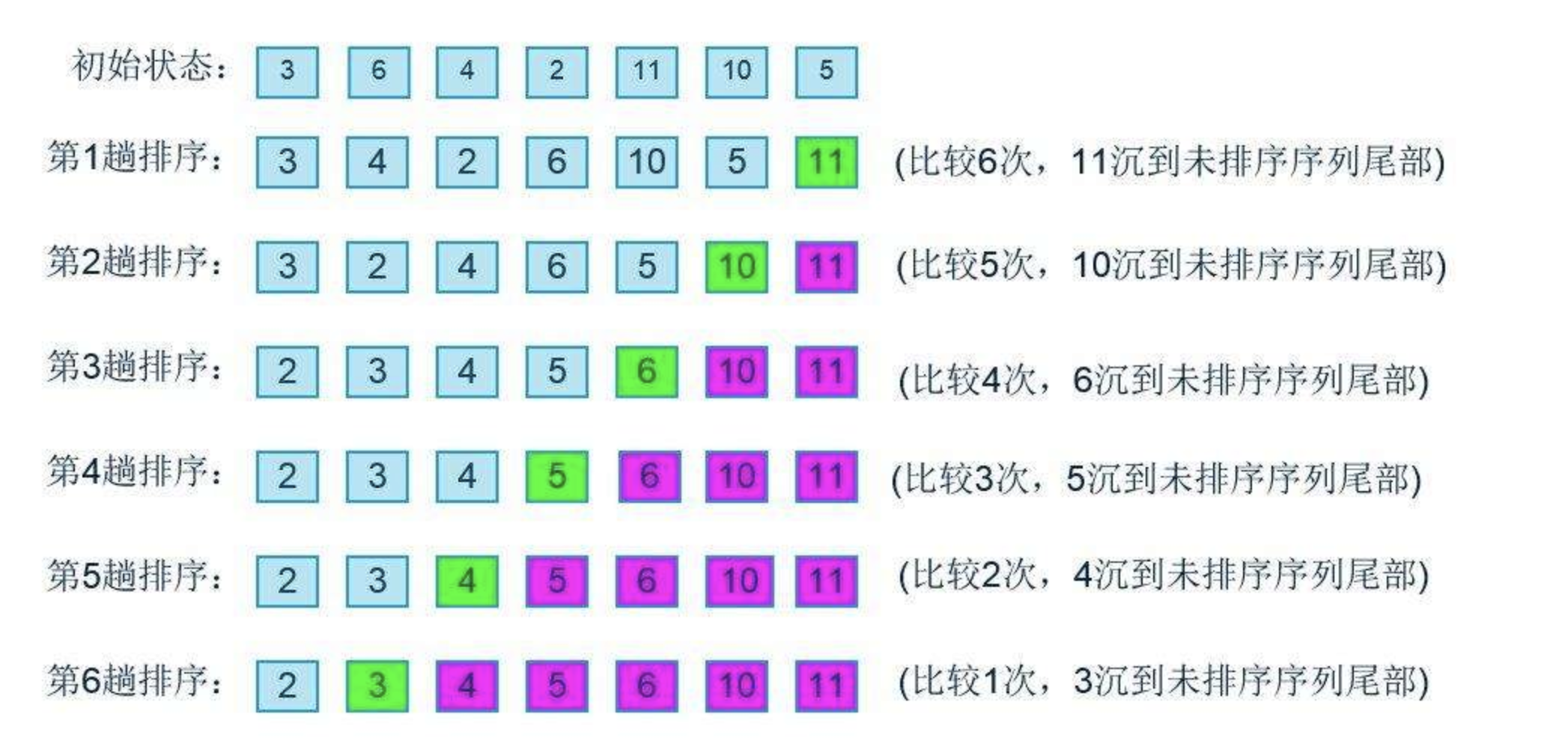
1.1、冒泡排序(O(n^2))
@Test
public void test(){
int nums[] = {49, 38, 65, 97, 76, 13, 27, 50};
冒泡排序(nums);
System.out.println(Arrays.toString(nums));
}
public void 冒泡排序(int[] nums) {
// i=> 排序次数(最多做n-1趟排序)
for (int i = 1; i < nums.length; i++) {
//j,当前位置指针 j最大不能超过 str.length - i
for (int j = 0; j < nums.length - i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
}
}
1.1.1、冒泡排序优化
public void 冒泡排序优化(int[] nums) {
// i=> 排序次数(最多做n-1趟排序)
for (int i = 1; i < nums.length; i++) {
//是否发生交换
boolean flag = false;
//j,当前位置指针 j最大不能超过 str.length - i
for (int j = 0; j < nums.length - i; j++) {
if (nums[j] > nums[j + 1]) {
flag = true;
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
//当一趟比较没有发送交换的时间表示已经有序
if (!flag) {
break;
}
}
}
1.2、选择排序
1、首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2、 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3、重复第二步,直到所有元素均排序完毕。
1、时间复杂度:(n^2)
@Test
public void test(){
int[] nums = {49, 38, 65, 97, 76, 13, 27, 50};
选择排序(nums);
System.out.println(Arrays.toString(nums));
}
public void 选择排序(int[] nums) {
//从前往后比较,从0开始,是因为它要赋值给min,i一直到a.length 也就是最后一个还需要往前移动
for (int i = 0; i < nums.length - 1; i++) {
//首先默认第一个为最小值
int idx = i;
//是和tId比较 ,不需要自己跟自己比较,min初始给的i,所以j=i+1;
for (int j = i + 1; j < nums.length; j++) {
if (nums[idx] > nums[j]) {
idx = j;
}
}
//每趟排序之后,idex的值都会不一样 ,而每次的min都是开始的i,所以当下的i和min进行替换
if (idx != i) {
int temp = nums[i];
nums[i] = nums[idx];
nums[idx] = temp;
}
}
}
1.3、直接插入排序(O(n^2))
从前往后走,每次和前面已经排好序的比较
1、时间复杂度O(n^2):
当问题规模为n时
最好情况(原本就是有序的)
比较次数:Cmin=n-1
移动次数:Mmin=0
最差情况(逆序)
比较次数:Cmax=1+2+3+4+……+n-1=(n-1)n/2
移动次数:Mmax=1+2+3+……+n-1=(n-1)n/2
若待排序对象序列中出现各种可能排列的概率相同,则可取上述最好情况和最坏情况的平均情况。在平均情况下的关键字比较次数和对象移动次数约为 n^2/4。(大O推导 1/4 可以去掉)因此,直接插入排序的时间复杂度为 o(n^2)。
2、空间复杂度:
插入排序过程中,需要一个临时变量temp存储待排序元素,因此空间复杂度为O(1)。
3、算法稳定性:
插入排序是一种稳定的排序算法。

1、直接插入排序 :从第二个开始,依次和前一个进行比较,插入一个有序序列(注意和选择排序的区别)
/**
* 1、直接插入排序 :个人理解,就是往后移动,依次把小的放到前面来
*/
@Test
public void insertionSort() {
int[] a = { 49, 38, 65, 97, 76, 13, 27, 50 };
System.out.println("----------插入排序开始:---------");
print(a);
for (int i = 1; i < a.length; i++) {//从i等于1开始表示a[1] 也即是从第二个数字开始进行比较,进行n-1趟排序
// 待插入元素
int temp = a[i];
int j ;
for (j = i; j > 0; j--)
{
// 将大于temp的往后移动一位,其实就是和temp进行比较移动,已经排序的二舅不会移动了
if (a[j-1] > temp)
{
a[j] = a[j-1]; //执行完这个 j之后还要 继续执行下一个 j 最后代表的就是 实际 带待插入元素的位置
}
else
{
break;
}
}
a[j] = temp; //,如果不变则原封不动给它(主要原因),如果变了则将它赋值给j 进行归为,此时的j就是我们上面排序之后找到的j的位置
System.out.printf("第"+i+"趟排序结果,");
print(a);
}
System.out.print("最终插入排序结果: ");
print(a);
System.out.println("--------------------");
}
/**
*
打印的结果
*/
private static void print(int []a) {
for (int i : a){
System.out.print(i + " ");
}
System.out.println();
}
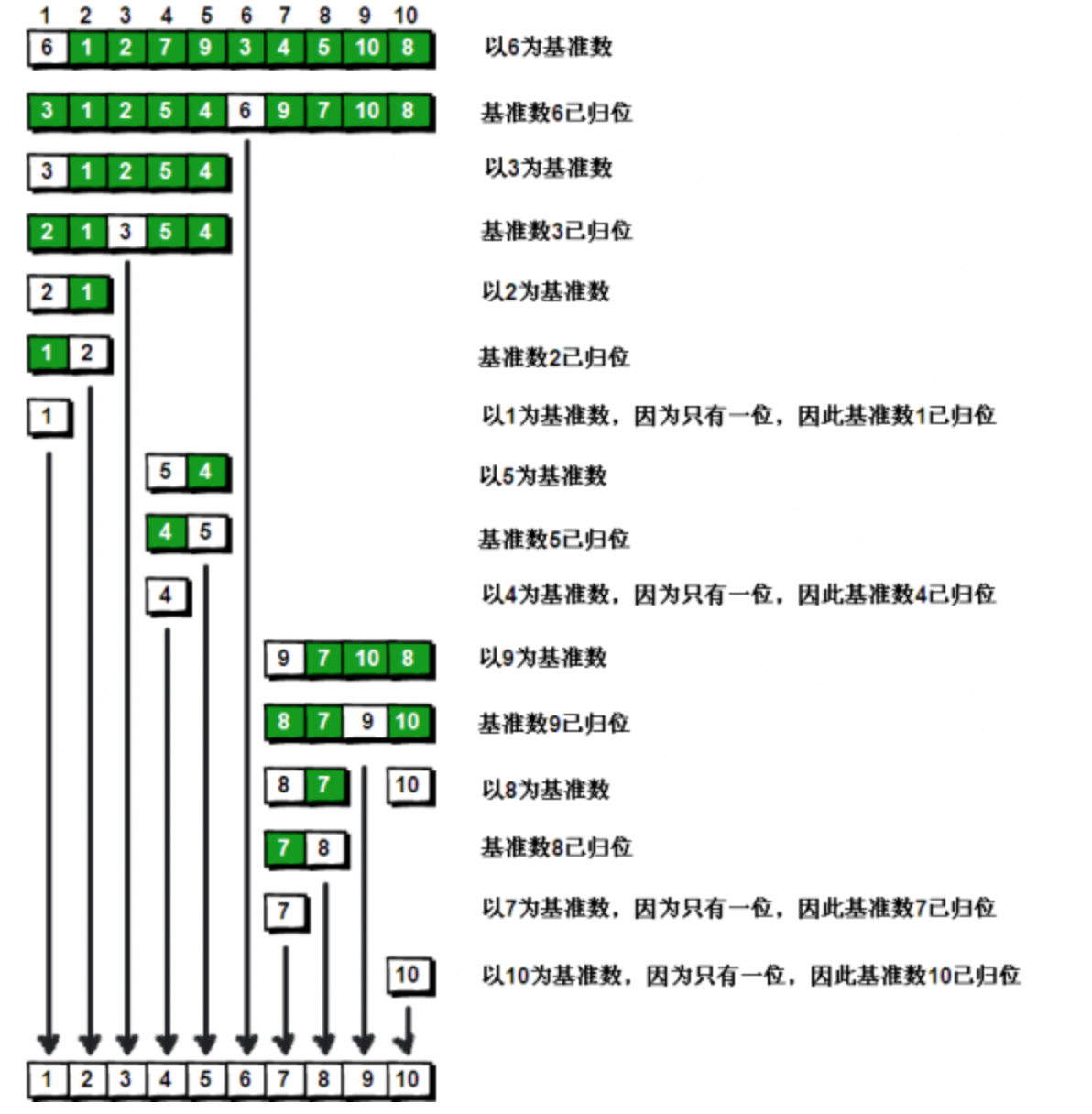
1.4、快速排序(O(log2^n))
1.先从数列中取出一个数作为基准数。下面
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
@Test
public void test() {
int nums[] = {49, 38, 65, 97, 76, 13, 27, 50};
快速排序(nums);
System.out.println(Arrays.toString(nums));
}
public void 快速排序(int[] nums) {
int low = 0;
int high = nums.length - 1;
sort(nums, low, high);
}
public void sort(int[] nums, int low, int high) {
int i = low, j = high;
//从左右两边交替扫描,直到left = right
if (i < j) {
//待排序的第一个元素作为基准值
int po = nums[low];
//每次当i比j小的时候小的时候开始比较,当它大于的时候,就会开始下一次排序
while (i < j) {
//从右往左扫描,找到第一个比基准值小的元素
while (i < j && po < nums[j]) {
j--;
}
//找到这种元素将nums[j]放入nums[i]中
nums[i] = nums[j];
//从左往右扫描,找到第一个比基准值大的元素
while (i < j && po > nums[i]) {
i++;
}
//找到这种元素将nums[i]放入nums[i]中
nums[j] = nums[i];
}
//基准值归位 这个时候 (这里i和j是相等的)
nums[i] = po;
//对基准值左边的元素进行递归排序(这里i和j是相等的)
sort(nums, low, i - 1);
//对基准值右边的元素进行递归排序。
sort(nums, i + 1, high);
}
}
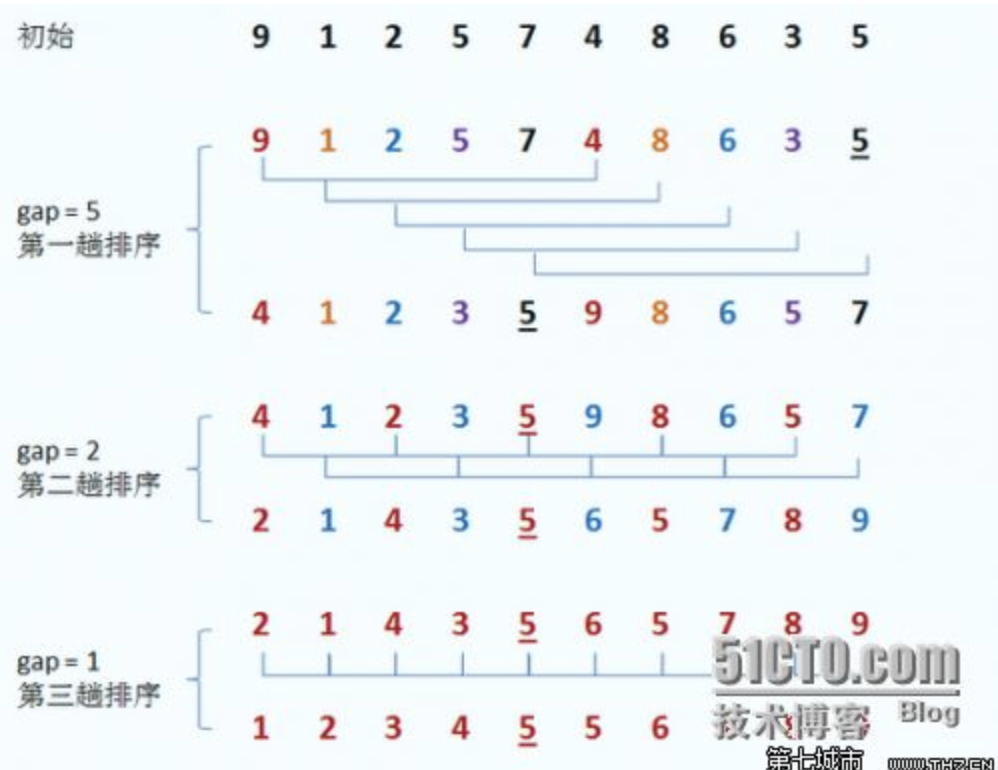
1.5、希尔排序(n^1.3)
@Test
public void test() {
int nums[] = {49, 38, 65, 97, 76, 13, 27, 50};
希尔排序(nums);
System.out.println(Arrays.toString(nums));
}
public void 希尔排序(int nums[]) {
//希尔排序增量,//被分成4组 ,也即是第1个和第5个进行比较 ,低2个和低6个比较
int incr = nums.length / 2;
//当增量为0的时候排序完成
while (incr > 0) {
//以为是从前往后第一个数字开始比较,所以初始化i=0 ,插入排序是从后往前比较, 小于a.length 表示的是有坑呢到最后分成最后一组的时候会 相互挨着的笔记,所以一定要到结尾
for (int i = 0; i < nums.length - 1; i++) {
// 这里的每一趟相当于是一次插入排序的排序算法,不同的是,这里是从前往后
for (int j = i; j < nums.length - incr; j = j + incr) {
if (nums[j] > nums[j + incr]) {
int temp = nums[j + incr];
nums[j + incr] = nums[j];
nums[j] = temp;
}
}
}
incr = incr / 2;
}
}
2、时间复杂度求法
https://www.cnblogs.com/dragondove/p/6389177.html
| 排序方法 | 最好 | 稳定 | 最坏 | 空间复杂度 | 稳定性 | 复杂性 | 特点 |
|---|---|---|---|---|---|---|---|
| 直接插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 | 简单 | 每次将一个待排序的数据,跟前面已经有序的序列的数字一一比较找到自己合适的位置,插入到序列中,直到全部数据插入完成。 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 | 复杂 | 先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。由于希尔排序是对相隔若干距离的数据进行直接插入排序,因此可以形象的称希尔排序为“跳着插” |
| 直接选择排序 | O(n) | O(n^2) | O(n^2) | O(1) | 不稳定 | 简单 | 数组分成有序区和无序区,初始时整个数组都是无序区,然后每次从无序区选一个最小的元素直接放到有序区的最后,直到整个数组变有序区。 |
| 快速排序 | O(nlog2n) | O(nlog2n) | O(n^2) | O(log2n) | 不稳定 | 复杂 | 1、n大时好,快速排序比较占用内存,内存随n的增大而增大,但却是效率高不稳定的排序算法。2、划分之后一边是一个,一边是n-1个,这种极端情况的时间复杂度就是O(N^2)3、最好的情况是每次都能均匀的划分序列,O(N*log2N) |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 | 简单 |
相关概念:
2.1、时间复杂度
时间复杂度可以认为是对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
常见的时间复杂度有:常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n2)
时间复杂度O(1):算法中语句执行次数为一个常数,则时间复杂度为O(1),
2.2、空间复杂度
空间复杂度是指算法在计算机内执行时所需存储空间的度量,它也是问题规模n的函数
空间复杂度O(1):当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1)
空间复杂度O(log2N):当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为O(log2n)
ax=N,则x=logaN,
空间复杂度O(n):当一个算法的空间复杂度与n成线性比例关系时,可表示为0(n).
2.3、排序时间复杂度的记忆法则
下面只是包含上面的排序算法的时间复杂度
快速最烦人
最差全部是n方
最好除快速为n,
快速最好为nLog
平均插入选择和冒泡为n方
快速依旧是nLog
希尔n的1.3次方
插入,冒泡最最稳定
稳定再加选择才简单
3、折半查找,二分查找O(log2n)
在已经有序的基础上进行查找
/**
* @Description
* @Author HealerJean
* @Date 2018/4/24 下午12:09.
*/
public class 折半查找 { //先有序,再折半查找
public static void main(String[] args) {
int array[]=new int[]{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,16,17,18,19,20};
int low=0;
int high=array.length-1;
int mid;
int x=20;
while(low<=high){ //最后的情况一定是相等
mid=(low+high)/2;
if(array[mid]==x){
System.out.println(x+"在数组中出现的位置"+mid);
break;
}
if(array[mid]<x){
low=mid+1;
}
if(array[mid]>x){
high=mid-1;
}
if(low>high){
System.out.println("查找失败");
break;
}
}
}
}


