前言

Github：https://github.com/HealerJean

博客：http://blog.healerjean.com

1、引入

问题：如果你负责开发维护一个大型的 网站，有一天老板找产品经理要网站每个网页每天的 PV、UV 数据，然后让你来开发这个统计模 块，你会如何实现?

1、PV统计：给每个网页一个独立的 Redis 计数器就可以了，这个计数器 的 key 后缀加上当天的日期。这样来一个请求，incrby 一次，最终就可以统计出所有的 PV 数据。

2、UV统计： 无脑解决方案：那就是为每一个页面一个独立的 set 集合来存储所 有当天访问过此页面的用户 ID。当一个请求过来时，我们使用 sadd 将用户 ID 塞进去就可以了。通过 scard 可以取出这个集合的大小，这个数字就是这个页面的 UV 数据。没错，这 是一个非常简单的方案。

以上解决方案带来带来的问题有哪些？

问题1：PV上面的方案是没有问题的，但是UV就有些low了？

答案：因为，如果你的页面访问量非常大，比如一个爆款页面几千万的 UV，你需要一个很大 的 set 集合来统计，这就非常浪费空间。 如果这样的页面很多，那所需要的存储空间是惊人 的。

问题2：为这样一个去重功能就耗费这样多的存储空间，值得么?

答案：当然不值得，如果数量很大很大，需要的数据基本上不需要太精确，差不多就行，105w 和 106w 这两个数字对于老板们来说并没有多大区别，

问题3：So，有没有更好的解决方案呢?

答案：Redis 提供了位图、 HyperLogLog 数据结构就是用来解决这种统计问题的。

1、redis位图

bitmap 同样是一种可以统计基数的方法，可以理解为用bit数组存储元素，例如01101001，表示的是[1,2,4,8]，bitmap中1的个数就是基数。bitmap也可以轻松合并多个集合，只需要将多个数组进行异或操作就可以了。

bitmap 相比于Set也大大节省了内存，我们来粗略计算一下，统计1亿个数据的基数，需要的内存是：100000000/8/1024/1024 ≈ 12M。

虽然bitmap在节省空间方面已经有了不错的表现，但是如果需要统计1000个对象，就需要大约12G的内存，显然这个结果仍然不能令我们满意。在这种情况下，HyperLogLog将会出来拯救我们。

2、HyperLogLog

HyperLogLog 提供不精确的去重计数方案，虽然不精确但是也不是非常不精确，标准误差是 0.81%，这样的精确度已经可以满足上面的 UV 统计需求了。

HyperLogLog 数据结构是 Redis 的高级数据结构，它非常有用，但是令人感到意外的 是，使用过它的人非常少。

2、使用方法

HyperLogLog 提供了两个指令 pfadd 和 pfcount，根据字面意义很好理解，一个是增加 计数，一个是获取计数。

◯ pfadd 用法和 set 集合的 sadd 是一样的，来一个用户 ID，就将用 户 ID 塞进去就是。

◯ pfcount 和 scard 用法是一样的，直接获取计数值。

127.0.0.1:6379> pfadd codehole user1 
(integer) 1
127.0.0.1:6379> pfcount codehole 
(integer) 1

127.0.0.1:6379> pfadd codehole user2
(integer) 1
127.0.0.1:6379> pfcount codehole 
(integer) 2

127.0.0.1:6379> pfadd codehole user3 
(integer) 1
127.0.0.1:6379> pfcount codehole 
(integer) 3

127.0.0.1:6379> pfadd codehole user4 
(integer) 1
127.0.0.1:6379> pfcount codehole 
(integer) 4

127.0.0.1:6379> pfadd codehole user5 
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 5

127.0.0.1:6379> pfadd codehole user6 
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 6

127.0.0.1:6379> pfadd codehole user7 user8 user9 user10 
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 10

3、验证

3.1、1000个数据

验证1000个数据，多久出现不一致

3.1.1、实例代码

@Test
public void test() {
  Jedis jedis = new Jedis("127.0.0.1", 6379);
  for (int i = 0; i < 1000; i++) {
    jedis.pfadd("codehole", "user" + i);

    long total = jedis.pfcount("codehole");
    if (total != i + 1) {
      log.info("total: {}, actually: {}", total, i + 1);
      break;
    }
  }
  jedis.close();
}



total: 99, actually: 100

3.1.2、归纳总结

当我们加入第 100 个元素时，结果开始出现了不一致，接下来我们将数据增加到 10w 个，看看总量差距有多大。

3.2、10w个数据

3.2.1、实例代码

@Test
public void test1000000() {
  Jedis jedis = new Jedis("127.0.0.1", 6379);
  for (int i = 0; i < 100000; i++) {
    jedis.pfadd("codehole", "user" + i);
  }
  long total = jedis.pfcount("codehole");
  log.info("total: {}, actually: {}", total, 100000);
  jedis.close();
}



total: 99725, actually: 100000

3.2.2、归纳总结

差了 275 个，按百分比是 0.275%，对于上面的 UV 统计需求来说，误差率也不算高。

然后我们把上面的脚本再跑一边，也就相当于将数据重复加入一边，查看输出，可以发现， pfcount 的结果没有任何改变，还是 99725，说明它确实具备去重功能。

4、pfmerge

HyperLogLog 除了上面的 pfadd 和 pfcount 之外，还提供了第三个指令 pfmerge，用于 将多个 pf 计数值累加在一起形成一个新的 pf 值。

比如在网站中我们有两个内容差不多的页面，运营说需要这两个页面的数据进行合并。 其中页面的 UV 访问量也需要合并，那这个时候 pfmerge 就可以派上用场了。

127.0.0.1:6379> pfadd h1 user1 user2 user3 user4 user5
(integer) 1
127.0.0.1:6379> pfcount h1
(integer) 5

127.0.0.1:6379> pfadd h2 user4 user5 user6
(integer) 1
127.0.0.1:6379> pfcount h2
(integer) 3
127.0.0.1:6379>


127.0.0.1:6379> pfmerge h3 h1 h2
OK
127.0.0.1:6379> pfcount h3
(integer) 6
127.0.0.1:6379>

5、HyperLogLog 原理

HyperLogLog，下面简称为HLL，它是 LogLog 算法的升级版，作用是能够提供不精确的去重计数。存在以下的特点：

1、代码实现较难。

2、能够使用极少的内存来统计巨量的数据，在 Redis 中实现的 HyperLogLog，只需要12K内存就能统计2^64个数据。

3、计数存在一定的误差，误差率整体较低。标准误差为 0.81% 。

3、误差可以被设置辅助计算因子进行降低。

问题：2^64个数据是多少k呢？

答案：取 Java 语言来说，一般long占用8字节，而一字节有8位，即：1 byte = 8 bit，即long数据类型最大可以表示的数是：2^63-1。对应上面的2^64个数，

假设此时有2^63-1这么多个数，从 0 ~ 2^63-1，按照long以及1k = 1024字节的规则来计算内存总数，就是：((2^63-1) * 8/1024)K，这是很庞大的一个数，存储空间远远超过12K。而 HyperLogLog 却可以用 12K 就能统计完。

5.1、注意事项

HyperLogLog 它需要占据 一定 12k 的存储空间(1k=1024B(字节)，一个英文占一个字节)，所以它不适合统计单个用户相关的数据。 因为如果你的用户上亿，可以算算，这个空间成本是非常惊人的。

不过你也不必过于担心，因为 Redis 对 HyperLogLog 的存储进行了优化，

1、在计数比较小时，它的存储空间采用稀疏矩阵存储，空间占用很小

2、仅仅在计数慢慢变大，稀疏矩阵占用空间渐渐超过了阈值时才会一次性转变成稠密矩阵，才会占用 12k 的空间。

5.2、原理分析

5.2.1、伯努利试验

在认识为什么HyperLogLog能够使用极少的内存来统计巨量的数据之前，要先认识下伯努利试验。伯努利试验是数学概率论中的一部分内容，它的典故来源于抛硬币。

伯努利试验：硬币拥有正反两面，一次的上抛至落下，最终出现正反面的概率都是50%。假设一直抛硬币，直到它出现正面为止，我们记录为一次完整的试验，中间可能抛了一次就出现了正面，也可能抛了4次才出现正面。无论抛了多少次，只要出现了正面，就记录为一次试验。这个试验就是伯努利试验。

1、那么对于多次的伯努利试验，假设这个多次为n次。就意味着出现了n次的正面。

2、假设每次伯努利试验所经历了的抛掷次数为k。第一次伯努利试验，次数设为k1，以此类推，第n次对应的是kn。

其中，对于这n次伯努利试验中，必然会有一个最大的抛掷次数k，例如抛了12次才出现正面，那么称这个为k_max，代表抛了最多的次数。

伯努利试验容易得出有以下结论：

1、n 次伯努利过程的投掷次数都不大于 k_max。

2、n 次伯努利过程，至少有一次投掷次数等于 k_max

最终结合极大似然估算的方法，发现在 n 和 k_max 中存在估算关联：n = 2^(k_max) 。这种通过局部信息预估整体数据流特性的方法似乎有些超出我们的基本认知，需要用概率和统计的方法才能推导和验证这种关联关系。 例如下面的样子：

第一次试验: 抛了3次才出现正面，此时 k=3，n=1
第二次试验: 抛了2次才出现正面，此时 k=2，n=2
第三次试验: 抛了6次才出现正面，此时 k=6，n=3
第n 次试验：抛了12次才出现正面，此时我们估算， n = 2^12

假设上面例子中实验组数共3组，那么 k_max = 6，最终 n=3，我们放进估算公式中去，明显： 3 ≠ 2^6 。也即是说，当试验次数很小的时候，这种估算方法的误差是很大的。

⬤ 在一次伯努利过程中，投掷次数大于k的概率为(1/2)^k，也就是投了k次反面的概率。

因此，一次过程中投掷次数不大于k的概率为1−(1/2)^k

因此 n次伯努利过程所有投掷次数都不大于k的概率为 P( x <= k_max) = (1−(1/2)^k_max)n

⬤ 进行 n 次伯努利过程，至少有一次大于等于 k_max 的概率：P( x >= k_max) = 1−(1−1/2^k_max−1)n

从上述公式中可得出结论：

1、当 n 远小于2^k_max时，P (x ≥ k_max) ≈ 0 ，即所有投掷次数都小于k；

2、当 n 远大于2^k_max时，P( X ≤ k_max) ≈ 0，即所有投掷次数都大于k。

因此，我们似乎就可以用2^kmax的值来粗略估计n的大小。 以上结论可以总结为：

进行了n次抛硬币实验，每次分别记录下第一次抛到正面的抛掷次数k，那么可以用n次实验中最大的抛掷次数 k_max 来预估实验组数量：n = 2^k_max

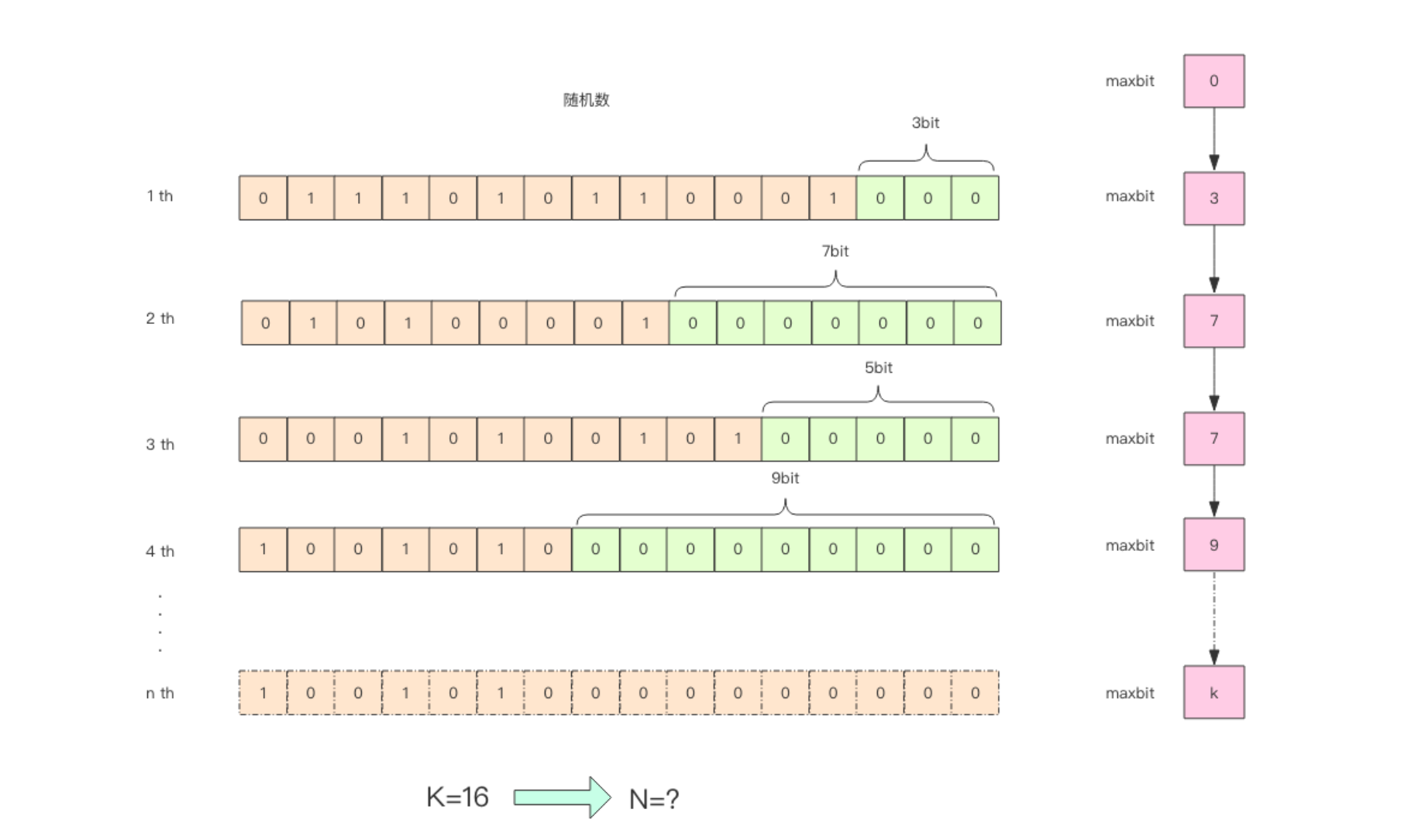
5.2.2、比特串的基数估计

问题：统计 APP或网页 的一个页面，每天有多少用户点击进入的次数。同一个用户的反复点击进入记为 1 次 。 但是这个怎么和 伯努利试验扯上关系呢

通过hash函数，将数据转为比特串，例如输入 5，便转为：101。

问题：为什么要这样转化呢？

答案：是因为要和抛硬币对应上，比特串中，0 代表了反面，1 代表了正面，如果一个数据最终被转化了 10010000，那么从右往左，从低位往高位看，我们可以认为，首次出现 1 的时候，就是正面。

那么基于上面的估算结论，我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验，同样也就可以根据存入数据中，转化后的出现了 1 的最大的位置 k_max 来估算存入了多少数据。

5.2.3、分桶平均

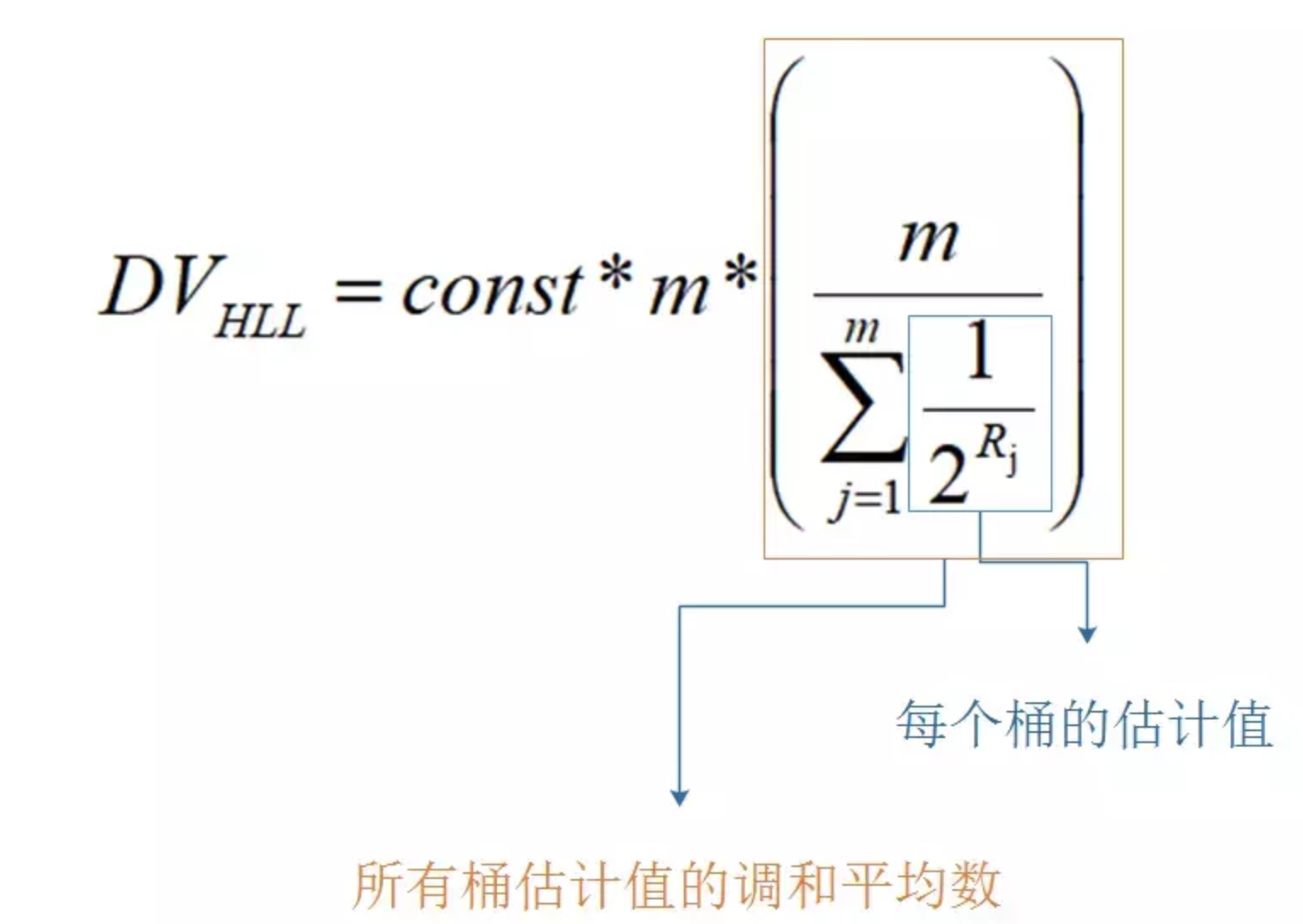
如果直接应用上面的HLL方法进行基数估计，会由于偶然性带来较大的误差，因此HLL算法采用分桶平均的方法来消减偶然性的误差、提高估计的准确度。

分桶就是分多少轮。抽象到计算机存储中去，就是存储的是一个以单位是比特(bit)，长度为 L 的大数组 S ，将 S 平均分为 m 组，注意这个 m 组，就是对应多少轮/桶，然后每组所占有的比特个数是平均的，设为 P。容易得出下面的关系：

☼ L = S.length

☼ L = m * p

☼ 以 K 为单位，S 占用的内存 = L / 8 / 1024

在 Redis 中，HyperLogLog设置为：m = 16834 ，p = 6，L = 16834 * 6 。占用内存为= 16834 * 6 / 8 / 1024 = 12K

  第0组     第1组                       .... 第16833组
[000 000] [000 000] [000 000] [000 000] .... [000 000]

5.2.3.1、举例

在这个统计问题中，不同的用户 id 标识了一个用户，那么我们可以把用户的 id 作为被hash的输入。即：hash(id) = 比特串 不同的用户 id，必然拥有不同的比特串。每一个比特串，也必然会至少出现一次 1 的位置。我们类比每一个比特串为一次伯努利试验。

分桶举例：

1、现在要分轮，也就是分桶。所以我们可以设定，每个比特串的前多少位转为10进制后，其值就对应于所在桶的标号。假设比特串的低两位用来计算桶下标志，此时有一个用户的 id 的比特串是：1001011000011。它的所在桶下标为：11(2) = 1*2^1 + 1*2^0 = 3，处于第3个桶，即第3轮中。

2、上面例子中，计算出桶号后，剩下的比特串是：10010110000，从低位到高位看，第一次出现 1 的位置是 5 。也就是说，此时第3个桶，第3轮的试验中，k_max = 5。5 对应的二进制是：101，又因为每个桶有 p 个比特位。当 p >= 3 时，便可以将 101 存进去。

3、模仿上面的流程，多个不同的用户 id，就被分散到不同的桶中去了，且每个桶有其 k_max。然后当要统计出 mian 页面有多少用户点击量的时候，就是一次估算。最终结合所有桶中的 k_max，代入估算公式，便能得出估算值。

真实场景举例：

先把数据分成若干个分组（桶bucket），估计每个分组的基数，然后用所有分组基数的平均数来估计总的基数。

Redis 中桶的个数是 2^14-1 = 16384，对于每个哈希值（64比特），14 位作为桶编号用来定位数据分布的桶位置，剩余的50 比特即伯努利过程，每个桶对应 6bit大小，记录 k_max。

举例说明，若UV值通过 Hash算法得到比特串“ 10110000 00000000 01101100 00000100 00101001 11000000 00000100 00011101”

1、后面14位确定桶编号：000100 00011101 ，即 bucket= 2^10+ 2^4 + 2^3 + 2^2 + 1 = 1053

2、前面的50比特伯努利过程：0110000 00000000 01101100 00000100 00101001 11000000 00 ，该例中 k_max = 9

3、那么UV基数估计为2^9

模仿上面的流程，代入估算公式，便能得出估算值。

5.2.3.2、占用的内存为什么是 12k

前面我们已经认识到，它的实现中，设有 16384 个桶，即：2^14 = 16384，每个桶有 6 位，存储 k_max，每个桶可以表达的最大二进制为： 111 111 ， 数字是：2^6-1 = 63 。

对于命令：pfadd key value

在存入时，value 会被 hash 成 64 位，即 64 bit 的比特字符串，前 14 位用来选择这个 value 的比特串中从右往左第一个 1 出现的下标位置数值要存到那个桶中去，即前 14 位用来分桶。设第一个1出现位置的数值为 index 。当 index = 5 时，就是: ....10000 [01 0000 0000 0000]

极端情况：

首先因为完整的 value 比特字符串是 64 位形式，减去 14 后，剩下 50 位，那么极端情况，出现 1 的位置，是在第 50 位，即位置是 50。此时 index = 50 。此时先将 index 转为 2 进制，它是：110010 。

因为16384 个桶中，每个桶是 6 bit 组成的 (50 < 2^6-1(111111) = 63 )。请注意，50 已经是最坏的情况，且它都被容纳进去了。那么其他的不用想也肯定能被容纳进去。

最终地，一个 key 所对应的 16384 个桶都设置了很多的 value 了，每个桶有一个k_max。此时调用 pfcount 时，按照前面介绍的估算方式，便可以计算出 key 的设置了多少次 value，也就是统计值。

value 被转为 64 位的比特串，最终被按照上面的做法记录到每个桶中去。64 位转为十进制就是：2^64，HyperLogLog 仅用了：16384 * 6 /8 / 1024 K 存储空间就能统计多达 2^64 个数。

5.2.3.3、重复的value

根据上面的做法，不同的 value，会被设置到不同桶中去

如果出现了在同一个桶的，即前 14 位值是一样的，但是后面出现 1 的位置不一样。那么比较新的 index 是否比原来的 index 大。是，则替换。否，则不变。

5.2.3.4、为什么要统计 Hash 值中第一个 1 出现的位置？

因为第一个 1 出现的位置可以同我们抛硬币的游戏中第一次抛到正面的抛掷次数对应起来，根据上面掷硬币实验的结论，记录每个数据的第一个出现的位置 K，就可以通过其中最大值 Kmax 来推导出数据集合中的基数：N = 2 ^Kmax

5.3、Redis 中的 HyperLogLog

从上面我们算是对 HyperLogLog 的算法和思想有了一定的了解，并且知道了一个 HyperLogLog 实际占用的空间大约是 12 KB，但 Redis 对于内存的优化非常变态

1、当计数比较小 的时候，大多数桶的计数值都是零，这个时候 Redis 就会适当节约空间，转换成稀疏存储方式

2、与之相对的，正常的存储模式叫做 密集存储，这种方式会恒定地占用 12 KB。

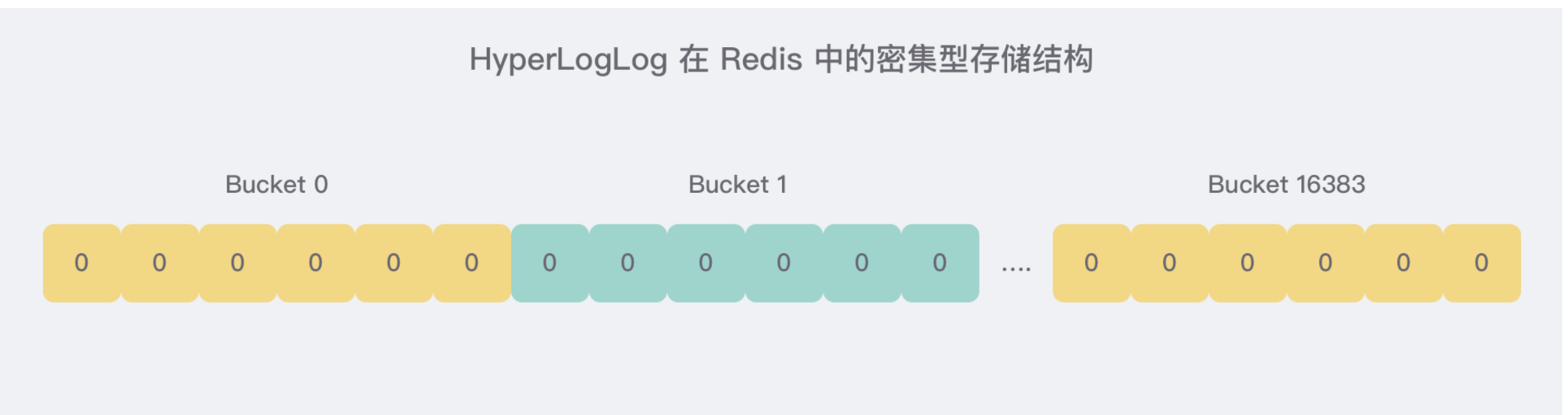
5.3.1、HLL_DENSE

密集存储的结构很简单，就是连续的16384个6比特连起来的位图。

5.3.2、HLL_SPARSE

稀疏存储针对的就是很多的桶计数值为0的情况，因此会有大量连续0的情况出现。

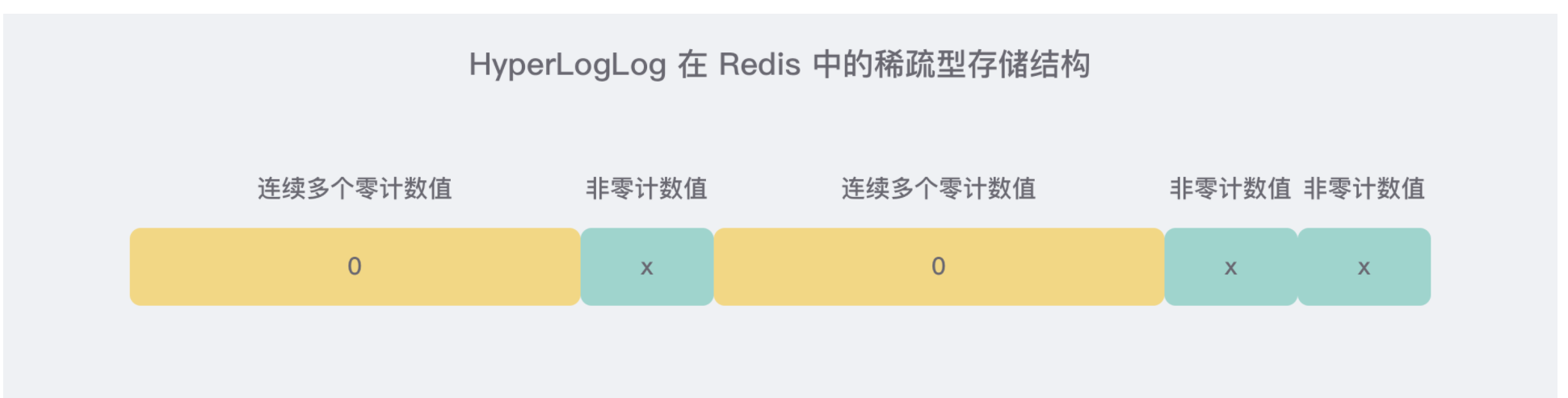
1、00xxxxxx：前缀两个零表示接下来的 6bit 整数值加 1 就是零值计数器的数量，注意这里要加 1 是因为数量如果为零是没有意义的。比如 00010101 表示连续 22 个零值计数器(2 ^ 4 + 2 ^ 2 + 1 + 1 = 22)。

2、01xxxxxx yyyyyyyy：6bit 最多只能表示连续 64 个零值计数器，这样扩展出的 14bit 可以表示最多连续 16384 个零值计数器。这意味着 HyperLogLog 数据结构中 16384 个桶的初始状态，所有的计数器都是零值，可以直接使用 2 个字节来表示。

3、1vvvvvxx：中间 5bit 表示计数值，尾部 2bit 表示连续几个桶。它的意思是连续 (xx +1) 个计数值都是 (vvvvv + 1)。比如 10101011 表示连续 4 个计数值都是 11。

只要以下条件满足其一，Redis就会从稀疏存储转换为密集存储：

1）任意一个桶的计数值(k_max)超过32；

2）稀疏存储占用的字节数超过 hll_sparse_max_bytes值，默认是3000字节（可配置调整）。